Advance-Data-Structure | RokoBasilisk's Blog

总结一部分数据结构

优先队列

特点

能保证每次取出的元素都是队列中优先级别最高的，优先级别是可以自定义的。评判标准如数值大小以及更加复杂的计算。

应用场景

从一堆杂乱无章的数据当中按照一定的顺序(或优先级)逐步筛选出部分乃至全部的数据。

For Example: 任意一个数组，找出前 k 大的数。

解法1：先对数组进行排序，然后依次输出前 k 大的数，复杂度将会是 O(nlogn)，其中 n 是数组的元素个数。

解法2：使用优先队列，复杂度优化成 O(k + nlogk)。当数据量很大(即 n 很大时)，而 k 相对较小，显然使用优先级队列可以有效地降低算法的复杂度。要找出前 k 大的数，不需要对所有的数进行排序。

实现

优先级的本质是一个二叉堆(Binary Heap)，利用一个数组结构来实现的完全二叉树。换句话说，优先队列的本质是一个数组，数组里的每个元素既有可能是其他元素的父节点，也有可能是其他元素的子节点，而且每个父节点只能有两个子节点，很像一个二叉树的结构。

若设二叉树的深度为k，除第 k 层外，其它各层 (1～k-1) 的结点数都达到最大个数，第k 层所有的结点都连续集中在最左边，这就是完全二叉树。

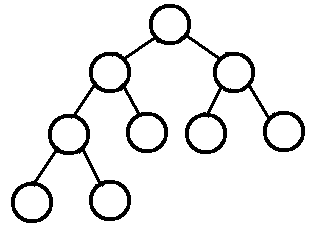
性质

数组里的第一个元素 array[0] 拥有最高的优先级别
给定一个下标 i ，那么对于元素 array[i] 而言：
- 它的父节点所对应的元素下标是 (i - 1) / 2
- 它的左孩子对应元素下标是 2 x i + 1
- 它的右孩子所对应的元素下标是 2 × i + 2
数组里每个元素的优先级别都要高于它两个孩子的优先级别。

操作

向上筛选( sift up / bubble up)

当有新的数据加入到优先队列中，新的数据首先被放置在二叉堆的底部。
不断进行向上筛选的操作，即如果发现该数据的优先级别比父节点的优先级别还要高，那么就和父节点的元素相互交换，再接着往上进行比较，直到无法再继续交换为止。

时间复杂度：由于二叉堆是一棵完全二叉树，并假设堆的大小为 k，因此整个过程其实就是沿着树的高度往上爬，所以只需要 O(logk) 的时间。

向下筛选( sift down / bubble down)

当堆顶的元素被取出时，要更新堆顶的元素来作为下一次按照优先级顺序被取出的对象，需要将堆底部的元素放置到堆顶，然后不断地对它执行向下筛选的操作。
将该元素和它的两个孩子节点对比优先级，如果优先级最高的是其中一个孩子，就将该元素和那个孩子进行交换，然后反复进行下去，直到无法继续交换为止。

时间复杂度：整个过程就是沿着树的高度往下爬，所以时间复杂度也是 O(logk)。

因此，无论是添加新的数据还是取出堆顶的元素，都需要 O(logk) 的时间。

初始化

优先队列的初始化是一个最重要的时间复杂度，是分析运用优先队列性能时必不可少的，也是经常容易弄错的地方。

举例：有 n 个数据，需要创建一个大小为 n 的堆。

误区：每当把一个数据加入到堆里，都要对其执行向上筛选的操作，这样一来就是 O(nlogn)。

解法：在创建这个堆的过程中，二叉树的大小是从 1 逐渐增长到 n 的，所以整个算法的复杂度经过推导，最终的结果是 O(n)。

初始化一个大小为 n 的堆，所需要的时间是 O(n) 。

E.g.: LeetCode 347: 给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

说明：

你可以假设给定的 k 总是合理的，且 1 ≤ k ≤ 数组中不相同的元素的个数。

你的算法的时间复杂度必须优于 O(nlogn) ，n 是数组的大小

示例：car，car，book，desk，desk，desk

解题思路

这道题的输入是一个字符串数组，数组里的元素可能会重复一次甚至多次，要求按顺序输出前 k 个出现次数最多的字符串。

解这类求”前 k 个”的题目，关键是看如何定义优先级以及优先队列中元素的数据结构。
题目中有”前 k 个“这样的字眼，应该很自然地联想到优先队列。
优先级别可以由字符串出现的次数来决定，出现的次数越多，优先级别越高，反之越低。
统计词频的最佳数据结构就是哈希表（Hash Map），利用一个哈希表，就能快速地知道每个单词出现的次数。
将单词和其出现的次数作为一个新的对象来构建一个优先队列，那么这个问题就很轻而易举地解决了。

建议：这道题是利用优先队列处理问题的典型，建议好好练习。

    Desk (3)
    /    \
car(2)   book(1)

图

基本知识点

图可以说是所有数据结构里面知识点最丰富的一个，最基本的知识点如下。

阶（Order）、度：出度（Out-Degree）、入度（In-Degree）
树（Tree）、森林（Forest）、环（Loop）
有向图（Directed Graph）、无向图（Undirected Graph）、完全有向图、完全无向图
连通图（Connected Graph）、连通分量（Connected Component）
存储和表达方式：邻接矩阵（Adjacency Matrix）、邻接链表（Adjacency List）

围绕图的算法也是五花八门。

图的遍历：深度优先、广度优先
环的检测：有向图、无向图
拓扑排序
最短路径算法：Dijkstra、Bellman-Ford、Floyd Warshall
连通性相关算法：Kosaraju、Tarjan、求解孤岛的数量、判断是否为树
图的着色、旅行商问题等

Important

必须掌握

图的存储和表达方式：邻接矩阵（Adjacency Matrix）、邻接链表（Adjacency List）
图的遍历：深度优先、广度优先
二部图的检测（Bipartite）、树的检测、环的检测：有向图、无向图
拓扑排序
联合-查找算法（Union-Find）
最短路径：Dijkstra、Bellman-Ford

其中，环的检测、二部图的检测、树的检测以及拓扑排序都是基于图的遍历，尤其是深度优先方式的遍历，而遍历可以在邻接矩阵或者邻接链表上进行。

至于最短路径算法，应该要能区分不同的特点，明确要用的算法。

E.g.： LeetCode 785：给定一个无向图 graph，当这个图为二部图时返回 true。

提示：如果能将一个图的节点集合分割成两个独立的子集 A 和 B，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为二部图。

解题思路：判断一个给定的任意图是否为二部图，就必须要对该图进行一次遍历：①深度优先；②广度优先

二部图，图的所有顶点可以分为两个子集 U 和 V，子集里的顶点互不直接相连，图里面所有边，一头连着子集 U 里的顶点，一头连着子集 V 里的顶点。

解析：

给图里的顶点涂上颜色，子集 U 里的顶点都涂上红色，子集 V 里的顶点都涂上蓝色。
开始遍历这个图的所有顶点，想象一下手里握有红色和蓝色的画笔，每次交替地给遍历当中遇到的顶点涂上颜色。
如果这个顶点还没有颜色，那就给它涂上颜色，然后换成另外一支画笔。
下一个顶点，如果发现这个顶点已经涂上了颜色，而且颜色跟我手里画笔的颜色不同，那么表示这个顶点它既能在子集 U 里，也能在子集 V 里。
所以，它不是一个二部图。

前缀树（Trie）

应用场景

前缀树被广泛地运用在字典查找当中，也被称为字典树。

举例：给定一系列字符串，这些字符串构成了一种字典，要求你在这个字典当中找出所有以“ABC”开头的字符串。

解法 1：暴力搜索

直接遍历一遍字典，然后逐个判断每个字符串是否由“ABC”开头。假设字典很大，有 N 个单词，要对比的不是“ABC”，而是任意的，那不妨假设所要对比的开头平均长度为 M，那么时间复杂度是 O(M×N)。

解法 2：前缀树

如果用前缀树头帮助对字典的存储进行优化，那么可以把搜索的时间复杂度下降为 O(M)，其中 M 表示字典里最长的那个单词的字符个数，在很多情况下，字典里的单词个数 N 是远远大于 M 的。因此，前缀树在这种场合中是非常高效的。

经典应用

网站上的搜索框会罗列出以搜索文字作为开头的相关搜索信息，这里运用了前缀树进行后端的快速检索。
汉字拼音输入法的联想输出功能也运用了前缀树。

举例：假如有一个字典，字典里面有如下词：”A”，”to”，”tea”，”ted”，”ten”，”i”，”in”，”inn”，每个单词还能有自己的一些权重值，那么用前缀树来构建这个字典将会是如下的样子：

性质

每个节点至少包含两个基本属性。
- children：数组或者集合，罗列出每个分支当中包含的所有字符
- isEnd：布尔值，表示该节点是否为某字符串的结尾
前缀树的根节点是空的
- 所谓空，即只利用到这个节点的 children 属性，即只关心在这个字典里，有哪些打头的字符。
除了根节点，其他所有节点都有可能是单词的结尾，叶子节点一定都是单词的结尾。

实现

前缀树最基本的操作就是两个：创建和搜索。

创建

遍历一遍输入的字符串，对每个字符串的字符进行遍历

从前缀树的根节点开始，将每个字符加入到节点的 children 字符集当中。

如果字符集已经包含了这个字符，则跳过。

如果当前字符是字符串的最后一个，则把当前节点的 isEnd 标记为真。

由上，创建的方法很直观。

前缀树真正强大的地方在于，每个节点还能用来保存额外的信息，比如可以用来记录拥有相同前缀的所有字符串。因此，当用户输入某个前缀时，就能在 O(1) 的时间内给出对应的推荐字符串。

搜索

与创建方法类似，从前缀树的根节点出发，逐个匹配输入的前缀字符，如果遇到了就继续往下一层搜索，如果没遇到，就立即返回。

例题分析

LeetCode 第 212 题：给定一个二维网格 board 和一个字典中的单词列表 words，找出所有同时在二维网格和字典中出现的单词。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。

说明：你可以假设所有输入都由小写字母 a-z 组成。

解题思路

这是一道出现较为频繁的难题，题目给出了一个二维的字符矩阵，然后还给出了一个字典，现在要求在这个字符矩阵中找到出现在字典里的单词。

由于字符矩阵的每个点都能作为一个字符串的开头，所以必须得尝试从矩阵中的所有字符出发，上下左右一步步地走，然后去和字典进行匹配，如果发现那些经过的字符能组成字典里的单词，就把它记录下来。

可以借用深度优先的算法来实现

解法

字典匹配的解法 1：每次都循环遍历字典，看看是否存在字典里面，如果把输入的字典变为哈希集合的话，似乎只需要 O(1) 的时间就能完成匹配。

但是，这样并不能进行前缀的对比，即，必须每次都要进行一次全面的深度优先搜索，或者搜索的长度为字典里最长的字符串长度，这样还是不够高效。

字典匹配的解法 2：对比字符串的前缀，借助前缀树来重新构建字典。

假如在矩阵里遇到了一个字符”V”，而字典里根本就没有以“V”开头的字符串，则不需要将深度优先搜索进行下去，可以大大地提高搜索效率。

构建好了前缀树之后，每次从矩阵里的某个字符出发进行搜索的时候，同步地对前缀树进行对比，如果发现字符一直能被找到，就继续进行下去，一步一步地匹配，直到在前缀树里发现一个完整的字符串，把它输出即可。

线段树(Segment Tree)

举例：假设有一个数组 array[0 … n-1]，里面有 n 个元素，现在要经常对这个数组做两件事。

更新数组元素的数值
求数组任意一段区间里元素的总和（或者平均值）

解法 1：遍历一遍数组。

时间复杂度 O(n)。

解法 2：线段树。

线段树，就是一种按照二叉树的形式存储数据的结构，每个节点保存的都是数组里某一段的总和。
适用于数据很多，而且需要频繁更新并求和的操作。

时间复杂度 O(logn)。

实现

举例：数组是 [1, 3, 5, 7, 9, 11]，那么它的线段树如下。

根节点保存的是从下标 0 到下标 5 的所有元素的总和，即 36。左右两个子节点分别保存左右两半元素的总和。按照这样的逻辑不断地切分下去，最终的叶子节点保存的就是每个元素的数值。

解法：

更新数组里某个元素的数值

从线段树的根节点出发，更新节点的数值，它保存的是数组元素的总和。修改的元素有可能会落在线段树里一些区间里，至少叶子节点是肯定需要更新的，所以，要做的是从根节点往下，判断元素的下标是否在左边还是右边，然后更新分支里的节点大小。因此，复杂度就是遍历树的高度，即 O(logn)。

对数组某个区间段里的元素进行求和

方法和更新操作类似，首先从根节点出发，判断所求的区间是否落在节点所代表的区间中。如果所要求的区间完全包含了节点所代表的区间，那么就得加上该节点的数值，意味着该节点所记录的区间总和只是所要求解总和的一部分。接下来，不断地往下寻找其他的子区间，最终得出所要求的总和。

建议：线段树的实现书写起来有些繁琐，需要不断地练习。

例题分析

LeetCode 第 315 题：给定一个整数数组 nums，按要求返回一个新数组 counts，使得数组 counts 有该性质——counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。

示例

输入：[5, 2, 6, 1]

输出：[2, 1, 1, 0]

解释

5 的右侧有 2 个更小的元素（2 和 1）
2 的右侧仅有 1 个更小的元素（1）
6 的右侧有 1 个更小的元素（1）
1 的右侧有 0 个更小的元素

解题思路

给定一个数组 nums，里面都是一些整数，现在要求打印输出一个新的数组 counts，counts 数组的每个元素 counts[i] 表示 nums 中第 i 个元素右边有多少个数小于 nums[i]。

例如，输入数组是 [5, 2, 6, 1]，应该输出的结果是 [2, 1, 1, 0]。

因为，对于 5，右边有两个数比它小，分别是 2 和 1，所以输出的结果中，第一个元素是 2；对于 2，右边只有 1 比它小，所以第二个元素是 1，类推。

如果使用线段树解法，需要理清线段树的每个节点应该需要包含什么样的信息。

线段树每个节点记录的区间是数组下标所形成的区间，然而对于这道题，因为要统计的是比某个数还要小的数的总和，如果把分段的区间设计成按照数值的大小来划分，并记录下在这个区间中的数的总和，就能快速地知道比当前数还要小的数有多少个。

首先，让从线段树的根节点开始，根节点记录的是数组里最小值到最大值之间的所有元素的总和，然后分割根节点成左区间和右区间，不断地分割下去。
初始化，每个节点记录的在此区间内的元素数量是 0，接下来从数组的最后一位开始往前遍历，每次遍历，判断这个数落在哪个区间，那么那个区间的数量加一。
遇到 1，把它加入到线段树里，此时线段树里各个节点所统计的数量会发生变化。
当前所遇到的最小值就是 1。
把 6 加入到线段树里。
求比 6 小的数有多少个，即查询线段树，从 1 到 5 之间有多少个数。
从根节点开始查询。由于所要查询的区间是 1 到 5，无法包含根节点的区间 1 到 6，所以继续往下查询。
左边，区间 1 到 3 被完全包含在 1 到 5 之间，把该节点所统计好的数返回。
右边，区间 1 到 5 跟区间 4 到 6 有交叉，继续往下看，区间 4 到 5 完全被包含在 1 到 5 之间，所以可以马上返回，并把统计的数量相加。
最后得出，在当前位置，在 6 的右边比 6 小的数只有一个。

通过这样的方法，每次把当前的数用线段树进行个数统计，然后再计算出比它小的数即可。算法复杂度是 O(nlogm)。

树状数组（Fenwick Tree / Binary Indexed Tree）

实现

举例：假设有一个数组 array[0 … n-1]，里面有 n 个元素，现在要经常对这个数组做两件事。

更新数组元素的数值
求数组前 k 个元素的总和（或者平均值）

解法 1：线段树。

线段树能在 O(logn) 的时间里更新和求解前 k 个元素的总和。

解法 2：树状数组。

该问题只要求求解前 k 个元素的总和，并不要求任意一个区间。
树状数组可以在 O(logn) 的时间里完成上述的操作。
相对于线段树的实现，树状数组显得更简单。

特点

树状数组的数据结构有以下几个重要的基本特征。

它是利用数组来表示多叉树的结构，在这一点上和优先队列有些类似，只不过，优先队列是用数组来表示完全二叉树，而树状数组是多叉树。
树状数组的第一个元素是空节点。
如果节点 tree[y] 是 tree[x] 的父节点，那么需要满足条件：y = x - (x & (-x))。

建议：由于树状数组所解决的问题跟线段树有些类似，所以不花篇幅进行问题的讨论。LeetCode 上有很多经典的题目可以用树状数组来解决，比如 LeetCode 第 308 题，求一个动态变化的二维矩阵里，任意子矩阵里的数的总和。

Conclusion

优先队列

经常出现在考题里的，它的实现过程比较繁琐，但是很多编程语言里都有它的实现，所以在解决面试中的问题时，实行“拿来主义”即可。

鼓励你自己练习实现一个优先队列，在实现它的过程中更好地去了解它的结构和特点。

被广泛运用的数据结构，很多涉及大数据的问题都得运用到图论的知识。

比如在社交网络里，每个人可以用图的顶点表示，人与人直接的关系可以用图的边表示；再比如，在地图上，要求解从起始点到目的地，如何行驶会更快捷，需要运用图论里的最短路径算法。

前缀树

出现在许多面试的难题当中。

因为很多时候你得自己实现一棵前缀树，所以你要能熟练地书写它的实现以及运用它。

线段树和树状数组

应用场合比较明确。

例如，问题变为在一幅图片当中修改像素的颜色，然后求解任意矩形区间的灰度平均值，那么可以考虑采用二维的线段树了。